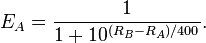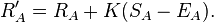[lang_fr]
Classement international (Classement Fide)
Classement National
Classement Rapide, classement blitz

Pièces d’un jeu d’ échecs.
Le classement Elo est un système d’évaluation du niveau d’un joueur d’échecs, ou de jeu de go, ou d’autres jeux à deux joueurs. Plus généralement, il peut servir à comparer deux joueurs avant une partie, et est utilisé par de nombreux jeux en ligne.
Elo se trouve parfois écrit par erreur en haut de casse ELO. Or, il ne s’agit pas d’un acronyme. Il doit son nom à Arpad Elo (1903-1992), un professeur de physique et excellent joueur d’échecs américain d’origine hongroise, qui l’a mis au point.
Sommaire |
Historique
La Fédération américaine du jeu d’échecs a utilisé le système d’Arpad Elo dès 1960. Il fut ensuite adopté par la FIDE (Fédération internationale des échecs) en 1970. Arpad Elo a décrit son travail dans les détails dans son livre The Rating of Chessplayers, Past and Present, publié en 1978.
Arpad Elo avait étudié la force des joueurs en se basant sur leurs résultats, et en avait déduit que leur force pouvait se mesurer par un classement en points distribué selon une loi normale de répartition.
Des tests statistiques ultérieurs ont montré que la force échiquéenne n’est pas tout à fait distribuée selon une loi normale. Aussi, l’USCF et la FIDE ont fait évoluer la formule de calcul vers une loi logistique. Cependant par respect pour la contribution du professeur Elo, le nom du classement international continue d’être appelé le « classement Elo ».
Théorie Elo
Le classement Elo est basé sur une mesure de la force relative des joueurs.
La force relative entre deux joueurs peut être déterminée facilement si ceux-ci ont disputé entre eux un nombre de parties suffisant pour être significatif. Le résultat statistique obtenu détermine en même temps une probabilité de gain pour les parties à venir entre ces deux mêmes joueurs.
L’idée du classement Elo est de convertir à l’aide d’une fonction la probabilité de gain d’un joueur contre un autre, en une mesure qui exprime l’écart de niveau entre eux et de pouvoir ainsi classer en théorie des joueurs qui ne se sont jamais rencontrés directement.
Le problème se pose dans les termes suivants : connaissant la probabilité de gain d’un joueur A contre un joueur B ainsi que celle de B contre un joueur C, quelle est la probabilité de gain de A contre C ?
 la probabilité de gain de A contre B.
la probabilité de gain de A contre B.
 la probabilité de gain de B contre C.
la probabilité de gain de B contre C.
 la probabilité théorique de gain de A contre C est telle que :
la probabilité théorique de gain de A contre C est telle que :

Le rapport entre la probabilité et son complément exprime la force relative f entre deux joueurs.
La force de A contre C est donc égale au produit des forces intermédiaires, celle de A contre B par celle de B contre C :
 avec
avec  et de la force peut se déduire la probabilité :
et de la force peut se déduire la probabilité : 
Exemple :
Avec q = 60 %, f (q ) = 0.60 / 0.40 = 1.5, A est une fois et demi plus fort que B.
Avec r = 66 % , f (r ) = 0 .66 / 0.33 = 2, B est deux fois plus fort que C.
f (p) = f (q) x f (r) = 1.5 x 2 = 3, A est trois fois plus fort que C.
Avec f ( p ) = 3 la probabilité de gain de A contre C est p = 3 / 4 soit 75 %.
La force f est une mesure, mais pour avoir un classement additif il faut une fonction ? (p) telle que : ?(p) = ?(q) + ?(r)
Autrement dit, l’écart mesuré entre A et C doit être égal à la somme des écarts mesurés entre A et B d’une part et B et C d’autre part, ce qui n’est pas le cas avec le produit des forces.
Posons ![\Delta ( p ) = t [ f ( p ) ] \;](http://upload.wikimedia.org/math/0/c/c/0cc0a14244cb20f4eabb350017319636.png) où t est une fonction à définir.
où t est une fonction à définir.
![\Delta ( p ) = \Delta ( q ) + \Delta ( r ) \Leftrightarrow t [ f (p) ] = t [ f (q) ] + t [ f (r) ] \;](http://upload.wikimedia.org/math/1/4/5/14533d9e2e4b77d4beb05f9bb8eed070.png)
![f ( p ) = f ( q ) \times f ( r ) \Rightarrow t [ f (q) \times f (r) ] = t [ f (q) ] + t [ f (r) ]](http://upload.wikimedia.org/math/5/e/a/5eac5ea039f51aab68311a0a8703ed08.png)
Cette transformation par t d’un produit en somme est la définition de la fonction logarithme, le logarithme décimal noté log est choisi pour t :
![\Delta ( p ) = log [ f (p) ] = log [ \frac {p}{1 - p} ]](http://upload.wikimedia.org/math/e/7/0/e707f93e44ef67f5240728f017b8e42e.png)
Pour étendre la plage de valeurs, un facteur multiplicatif fixé à 400 est introduit.
On obtient la formule Elo : 
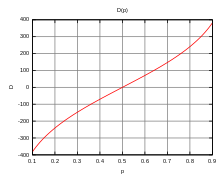
D(p)
Exemple :
- Avec q = 0.60 et r = 0.66, les forces sont f(q) = 1.5, f(r) = 2 et f(p) = 3.
? (q) = 400 x log ( 1.5 ) = 400 x 0.176 = 70.4 ? (r) = 400 x log ( 2 ) = 400 x 0.301 = 120.4 ? (p) = 400 x log ( 3 ) = 400 x 0.477 = 190.8
Nous avons bien ? (p) = 70.4 + 120.4 = 190.8

p(D)
La fonction réciproque p (D) donne la probabilité de gain en fonction de la différence Elo D :

Cette fonction est comprise entre 0 et 1 et vaut 0.5 en D=0.
Aux échecs, la fonction p (d) est utilisée pour calculer le nouvel Elo En+1 en fonction de l’ancien En :

W est le résultat de la partie : 1 pour une victoire, 0.5 pour un nul et 0 pour une défaite.
p (D) représente le résultat attendu de la part du joueur en fonction de la différence D avec son adversaire.
La différence W – p (D) traduit l’écart entre résultat effectif et résultat attendu.
K est un coefficient de développement : 25 pour les 30 premières parties, 15 tant que le joueur est en dessous de 2400 points Elo et définitivement 10 ensuite.
Exemple : un joueur classé 1800 fait nul contre un joueur classé 2005.



Nombre de GMI par tranche de 10 points Elo (Juillet 2009).
En pratique la FIDE limite ses calculs en plafonnant D à 400 points, c’est-à-dire que s’il y a plus de 400 points d’écart, donc plus de 91 % de chances de gain théoriques, la différence est ramenée à 400 points.
Du facteur K dépend la volatilité du classement, plus K est élevé et plus les variations du classement seront amplifiées. Cela pour permettre aux nouveaux joueurs entrants dans le classement de progresser rapidement vers leur niveau réel. Les joueurs anciens dans le classement ont un facteur K moins élevé et les joueurs qui ont atteint un Elo supérieur à 2400 ont leur facteur K au minimum.
Historiquement à l’initialisation du processus en 1970, il fut décidé que tous les grands maîtres internationaux du monde avaient un classement de 2 500 points Elo. C’est à partir de cette base de joueurs initiale que le classement s’est progressivement calculé pour tous les autres joueurs.
Mode de calcul
Les fédérations nationales utilisent souvent un système légèrement différent de celui de la Fédération internationale des échecs (FIDE).
Il existe souvent deux classements distincts : l’un au niveau international, géré par la FIDE, et dit « Classement FIDE » ou « Classement international », et un au niveau national, géré en France par la FFE, par la FQE au Québec, par la FCE au Canada et par la FSE en Suisse, dit « Elo national ». Un joueur peut disposer à la fois d’un classement international et d’un ou plusieurs classements nationaux qui évoluent indépendamment.
Jusqu’en 1993, le seuil minimal du classement FIDE était fixé à 2200, soit le niveau d’un candidat maître, les amateurs ne disposaient que du classement national. Il a été abaissé progressivement jusqu’à atteindre 1200 depuis le 1er juillet 2009, soit le niveau d’un joueur de club débutant, et l’intention de la FIDE est de le baisser jusqu’à 1000, qui est le niveau d’un débutant en tout début d’apprentissage, soit in fine la totalité des joueurs.
Depuis le 1er juillet 2009, la différence maximale entre deux classements pour le calcul des points gagnés ou perdus après chaque partie a été ramenée à 400 points au lieu de 350 précédemment.
Calcul du classement FIDE

Nombre de classés FIDE par tranche de 10 points Elo (juillet 2009).
- Premier classement
Dans un système suisse où le joueur rencontre au moins trois joueurs classés FIDE :
- on détermine le classement moyen des adversaires, Rc.
- on calcule le pourcentage de gain contre ces adversaires, p (c’est-à-dire la somme des points obtenus divisée par le nombre de parties)
- on détermine d(p) en fonction de la table FIDE 3
- si p < 0,5, alors Ru=Rc + d(p)
- si p = 0,5, alors Ru=Rc
- si p > 0,5, alors Ru=Rc + 12,5 points par demi-point obtenu au-dessus de 50 %
Dès qu’il existe 9 parties jouées, le premier classement publié sera égal à la moyenne pondérée des Ru de chaque tournoi, arrondie à l’entier le plus proche, si toutefois celle-ci dépasse 1200 (seuil plancher au 1er juillet 2009).
Par exemple, un joueur qui joue trois tournois :
- dans le premier, il réalise un Ru= 2280 sur 5 parties
- dans le second, Ru= 2400 sur 10 parties
- dans le troisième, Ru= 2000 sur 5 parties
Son premier classement sera :
- Rn = ( 2280 × 5 + 2400 × 10 + 2000 × 5 ) / 20 = 2270.
- Classement habituel
Pour chaque partie jouée contre un joueur classé FIDE :
- on détermine la différence d de classement entre le joueur adverse et le sien (ramenée à 400 si elle dépasse 400 depuis le 1er juillet 2009 – au lieu de 350 avant cette date)
- on détermine p(d) à l’aide de la table FIDE 3
- on détermine un coefficient K qui vaudra :
- K=25 jusqu’à la 30e partie du joueur, sinon
- K=15 pour un classement Elo en dessous de 2400 Elo, sinon
- K=10 pour un classement Elo au-dessus de 2400.
- soit W le résultat contre l’adversaire (W=1, ½ ou 0), le nouveau classement sera :
- Rn = Ro + K x (W – p(d))
Par exemple, si un joueur classé 2600 gagne contre un joueur classé 2700, son nouveau classement sera : 2600 + 10 × ( 1 – 0,36 ) = 2606,4. Pour la publication, on arrondira à l’entier le plus proche.
Le classement FIDE est mis à jour tous les deux mois , et publié le 1er janvier, 1er mars, 1er mai et 1er juillet, 1er septembre, 1er novembre. Si un joueur a moins de quatre parties classées sur une période d’un an, il est considéré comme inactif. Si le classement passe en dessous du seuil FIDE (1200), le joueur est retiré de la liste et à nouveau considéré comme un non-classé.
- Performance Elo
On utilise la notion de performance Elo pour caractériser la force d’un joueur dans un tournoi, en fonction de la moyenne des classements Elo des adversaires (Rc) et du résultat contre ceux-ci (p), elle est aussi parfois employée comme système de départage d’un tournoi au système suisse :
- Rp=Rc + d(p)
Statistiques
Au 1er septembre 2010 :
- Joueur classé premier le plus de fois : Garry Kasparov (23 fois)
- Plus jeune joueur classé parmi les 100 premiers : Anish Giri 2 677 points (16 ans – no 61)
- Plus jeune joueur parmi les 10 premiers : Magnus Carlsen 2 826 points (20 ans – no 1)
- Plus vieux joueur classé parmi les 100 premiers : Kiril Georgiev (45 ans – no 51) et Nigel Short (45 ans – no 48)
Au 1er mars 2011 , seuls 6 joueurs avaient dépassé les 2 800 points, soit avec indication du Elo le plus élevé : Garry Kasparov (2 851), Magnus Carlsen (2 826) , Viswanathan Anand (2 817), Veselin Topalov (2 813), Vladimir Kramnik (2 811), et Levon Aronian (2 808).
Niveau de jeu en fonction du nombre de points
Ces éléments sont donnés à titre indicatif. Les titres sont attribués par la FIDE en fonction de performances réalisées lors de compétitions et si le prétendant a obtenu un classement Elo requis. Ils sont ensuite acquis à vie et le classement d’un maître peut ensuite être inférieur à ce minimum.
- > 1000 : Débutant (enfant)
- > 1200 : Débutant
- > 1400 : Joueur amateur
- > 1600 : Bon joueur
- > 1800 : Très bon joueur
- > 2000 : Niveau national
- > 2200 : candidat maître
- > 2300 : Maître FIDE
- > 2400 : Maître international (~ 2 565 joueurs)
- > 2500 : Grand maître international (~ 1 200 joueurs)
- > 2600 : Les 200 meilleurs joueurs mondiaux
- > 2700 : Les 30 meilleurs joueurs mondiaux
- > 2800 : Seuls Garry Kasparov, Vladimir Kramnik, Veselin Topalov, Viswanathan Anand, Magnus Carlsen et Levon Aronian ont dépassé les 2 800 points
Les numéros un mondiaux
Depuis l’adoption du classement par la FIDE en 1970, seuls sept joueurs ont été classés à la première place. Garry Kasparov est le joueur ayant obtenu le plus haut classement et celui étant resté numéro un le plus longtemps.
Le classement Elo maximum indiqué est celui de la période considérée (ce qui ne correspond pas toujours au meilleur classement Elo du joueur)
[/lang_fr]
[lang_en]
Elo rating system

Chess
The Elo rating system is a method for calculating the relative skill levels of players in two-player games such as chess. It is named after its creator Arpad Elo, a Hungarian-born American physics professor.
The Elo system was invented as an improved chess rating system, but today it is also used in many other games. It is also used as a rating system for multiplayer competition in a number of computer games, [1] and has been adapted to team sports including association football, American college football and basketball, and Major League Baseball.
Contents
|
History
Arpad Elo was a master-level chess player and an active participant in the United States Chess Federation (USCF) from its founding in 1939. [2] The USCF used a numerical ratings system, devised by Kenneth Harkness, to allow members to track their individual progress in terms other than tournament wins and losses. The Harkness system was reasonably fair, but in some circumstances gave rise to ratings which many observers considered inaccurate. On behalf of the USCF, Elo devised a new system with a more statistical basis.
Elo’s system replaced earlier systems of competitive rewards with a system based on statistical estimation. Rating systems for many sports award points in accordance with subjective evaluations of the ‘greatness’ of certain achievements. For example, winning an important golf tournament might be worth an arbitrarily chosen five times as many points as winning a lesser tournament.
A statistical endeavor, by contrast, uses a model that relates the game results to underlying variables representing the ability of each player.
Elo’s central assumption was that the chess performance of each player in each game is a normally distributed random variable. Although a player might perform significantly better or worse from one game to the next, Elo assumed that the mean value of the performances of any given player changes only slowly over time. Elo thought of a player’s true skill as the mean of that player’s performance random variable.
A further assumption is necessary, because chess performance in the above sense is still not measurable. One cannot look at a sequence of moves and say, « That performance is 2039. » Performance can only be inferred from wins, draws and losses. Therefore, if a player wins a game, he is assumed to have performed at a higher level than his opponent for that game. Conversely if he loses, he is assumed to have performed at a lower level. If the game is a draw, the two players are assumed to have performed at nearly the same level.
Elo did not specify exactly how close two performances ought to be to result in a draw as opposed to a win or loss. And while he thought it is likely that each player might have a different standard deviation to his performance, he made a simplifying assumption to the contrary.
To simplify computation even further, Elo proposed a straightforward method of estimating the variables in his model (i.e., the true skill of each player). One could calculate relatively easily, from tables, how many games a player is expected to win based on a comparison of his rating to the ratings of his opponents. If a player won more games than he was expected to win, his rating would be adjusted upward, while if he won fewer games than expected his rating would be adjusted downward. Moreover, that adjustment was to be in exact linear proportion to the number of wins by which the player had exceeded or fallen short of his expected number of wins.
From a modern perspective, Elo’s simplifying assumptions are not necessary because computing power is inexpensive and widely available. Moreover, even within the simplified model, more efficient estimation techniques are well known. Several people, most notably Mark Glickman, have proposed using more sophisticated statistical machinery to estimate the same variables. On the other hand, the computational simplicity of the Elo system has proven to be one of its greatest assets. With the aid of a pocket calculator, an informed chess competitor can calculate to within one point what his next officially published rating will be, which helps promote a perception that the ratings are fair.
Implementing Elo’s scheme
[Top page]
The USCF implemented Elo’s suggestions in 1960, [3] and the system quickly gained recognition as being both more fair and more accurate than the Harkness rating system. Elo’s system was adopted by FIDE in 1970. Elo described his work in some detail in the book The Rating of Chessplayers, Past and Present, published in 1978.
Subsequent statistical tests have shown that chess performance is almost certainly not normally distributed. Weaker players have significantly greater winning chances than Elo’s model predicts. Therefore, both the USCF and FIDE have switched to formulas based on the logistic distribution. However, in deference to Elo’s contribution, both organizations are still commonly said to use « the Elo system ».
Different ratings systems
[Top page]
The phrase « Elo rating » is often used to mean a player’s chess rating as calculated by FIDE. However, this usage is confusing and often misleading, because Elo’s general ideas have been adopted by many different organizations, including the USCF (before FIDE), the Internet Chess Club (ICC), Yahoo! Games, and the now-defunct Professional Chess Association (PCA). Each organization has a unique implementation, and none of them precisely follows Elo’s original suggestions. It would be more accurate to refer to all of the above ratings as Elo ratings, and none of them as the Elo rating.
Instead one may refer to the organization granting the rating, e.g. « As of August 2002, Gregory Kaidanov had a FIDE rating of 2638 and a USCF rating of 2742. » It should be noted that the Elo ratings of these various organizations are not always directly comparable. For example, someone with a FIDE rating of 2500 will generally have a USCF rating near 2600 and an ICC rating in the range of 2500 to 3100.
FIDE ratings
[Top page]
For top players, the most important rating is their FIDE rating. Since July 2009, FIDE issues a ratings list once every two months.
The following analysis of the January 2006 FIDE rating list gives a rough impression of what a given FIDE rating means:
- 17171 players had a rating between 2200 and 2399, and are usually associated with the Candidate Master or FIDE Master title.
- 1868 players had a rating between 2400 and 2499, most of whom had either the International Master or the International Grandmaster title.
- 563 players had a rating between 2500 and 2599, most of whom had the International Grandmaster title
- 123 players had a rating between 2600 and 2699, all but one of whom had the International Grandmaster title
- 17 players had a rating between 2700 and 2799 (35 in March 2011)
- 2 players had a rating over 2800 (3 in March 2011)
The highest ever FIDE rating was 2851, which Garry Kasparov had on the July 1999 and January 2000 lists. A list of highest ever rated players is at Methods for comparing top chess players throughout history.
Performance rating
| p | dp |
|---|---|
| 0.99 | +677 |
| 0.9 | +366 |
| 0.8 | +240 |
| 0.7 | +149 |
| 0.6 | +72 |
| 0.5 | 0 |
| 0.4 | -72 |
| 0.3 | -149 |
| 0.2 | -240 |
| 0.1 | -366 |
| 0.01 | -677 |
Performance Rating is a hypothetical rating that would result from the games of a single event only. Some chess organizations use the « algorithm of 400 » to calculate performance rating. According to this algorithm, performance rating for an event is calculated by taking (1) the rating of each player beaten and adding 400, (2) the rating of each player lost to and subtracting 400, (3) the rating of each player drawn, and (4) summing these figures and dividing by the number of games played. This can be expressed by the following formula:
- Performance rating = [(Total of opponents’ ratings + 400 * (Wins – Losses)) / Games].
This is a simplification because it doesn’t take account of k-factors. But it offers an easy way to get an estimate of PR (Performance Rating).
FIDE, however, calculates performance rating by means of the formula: Opponents’ Rating Average + Rating Difference. Rating Difference dp is based on a player’s tournament percentage score p, which is then used as the key in a lookup table. p is simply the number of points scored divided by the number of games played. Note that, in case of a perfect or no score dp is indeterminate. The full table can be found in the edit] FIDE tournament categories
| Category | Average rating | |
|---|---|---|
| Minimum | Maximum | |
| 16 | 2626 | 2650 |
| 17 | 2651 | 2675 |
| 18 | 2676 | 2700 |
| 19 | 2701 | 2725 |
| 20 | 2726 | 2750 |
| 21 | 2751 | 2775 |
| 22 | 2776 | 2800 |
FIDE classifies tournaments into categories according to the average rating of the players. Each category is 25 rating points wide. Category 1 is for an average rating of 2251 to 2275, category 2 is 2276 to 2300, etc. For women’s tournaments, the categories are 200 rating points lower, so a Category 1 is an average rating of 2051 to 2075, etc. [4] The highest rated tournaments have been category 22, with an average from 2776 to 2800. The top categories are in the table.
Live ratings
[Top page]
FIDE updates its ratings list every two months. In contrast, the unofficial « Live ratings » calculate the change in players’ ratings after every game. These Live ratings are based on the previously published FIDE ratings, so a player’s Live rating is intended to correspond to what the FIDE rating would be if FIDE were to issue a new list that day.
Although Live ratings are unofficial, interest arose in Live ratings in August/September 2008 when five different players took the « Live » #1 ranking. [5]
The unofficial live ratings are published and maintained by Hans Arild Runde at edit] United States Chess Federation ratings
The United States Chess Federation (USCF) uses its own classification of players: [6]
- 2400 and above: Senior Master
- 2200–2399 plus 300 games above 2200: Original Life Master [7]
- 2200–2399: National Master
- 2000–2199: Expert
- 1800–1999: Class A
- 1600–1799: Class B
- 1400–1599: Class C
- 1200–1399: Class D
- 1000–1199: Class E
- 800-999: Class F
- 600-799: Class G
- 400-599: Class H
- 200-399: Class I
- 100-199: Class J
In general, 1000 is considered a bright beginner. In 2007, the median rating of all USCF members was 657.
The K factor, in the USCF rating system, can be estimated by dividing 800 by the effective number of games a player’s rating is based on (Ne) plus the number of games the player completed in a tournament (m). [9]
Rating floors
[Top page]
The USCF maintains an absolute ratings floor of 100 for all ratings. Thus, no member can have a rating below 100, no matter their performance at USCF sanctioned events. However, players can have higher individual absolute ratings floors, calculated using the following formula:
- AF = min(100 + 4NW + 2ND + NR,150)
where NW is the number of rated games won, ND is the number of rated games drawn, and NR is the number of events in which the player completed three or more rated games.
Higher rating floors exist for experienced players who have achieved significant ratings. Such higher rating floors exist, starting at ratings of 1200 in 100 point increments up to 2100 (1200, 1300, 1400, … , 2100). A player’s rating floor is calculated by taking their peak rating, subtracting 200 points, and then rounding down to the nearest rating floor. For example, a player who has reached a peak rating of 1464 would have a rating floor of 1464 – 200 = 1264, which would be rounded down to 1200. Under this scheme, only Class C players and above are capable of having a higher rating floor than their absolute player rating. All other players would have a floor of at most 150.
There are two ways to achieve higher rating floors other than under the standard scheme presented above. If a player has achieved the rating of Original Life Master, his or her rating floor is set at 2200. The achievement of this title is unique in that no other recognized USCF title will result in a new floor. For players with ratings below 2000, winning a cash prize of $2,000 or more raises that player’s rating floor to the closest 100-point level that would have disqualified the player for participation in the tournament. For example, if a player won $4,000 in a 1750 and under tournament, the player would now have a rating floor of 1800.
Ratings of computers
Since 2005–2006, human-computer chess matches have demonstrated that chess computers are capable of defeating even the strongest human players ( Deep Blue versus Garry Kasparov). However ratings of computers are difficult to quantify. There have been too few games under tournament conditions to give computers or software engines an accurate rating. [10] Also, for chess engines, the rating is dependent on the machine a program runs on.
For some ratings estimates, see Chess Engine.
Theory
Mathematical details

Professor Arpad Elo, inventor of the system
Performance can’t be measured absolutely; it can only be inferred from wins, losses, and draws against other players. A player’s rating depends on the ratings of his or her opponents, and the results scored against them. The relative difference in rating between two players determines an estimate for the expected score between them. Both the average and the spread of ratings can be arbitrarily chosen. Elo suggested scaling ratings so that a difference of 200 rating points in chess would mean that the stronger player has an expected score (which basically is an expected average score) of approximately 0.75, and the USCF initially aimed for an average club player to have a rating of 1500.
A player’s expected score is his probability of winning plus half his probability of drawing. Thus an expected score of 0.75 could represent a 75% chance of winning, 25% chance of losing, and 0% chance of drawing. On the other extreme it could represent a 50% chance of winning, 0% chance of losing, and 50% chance of drawing. The probability of drawing, as opposed to having a decisive result, is not specified in the Elo system. Instead a draw is considered half a win and half a loss.
If Player A has true strength RA and Player B has true strength RB, the exact formula (using the logistic curve) for the expected score of Player A is
Similarly the expected score for Player B is
This could also be expressed by
and
where  and
and 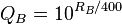 . Note that in the latter case, the same denominator applies to both expressions. This means that by studying only the numerators, we find out that the expected score for player A is QA / QB times greater than the expected score for player B. It then follows that for each 400 rating points of advantage over the opponent, the chance of winning is magnified ten times in comparison to the opponent’s chance of winning.
. Note that in the latter case, the same denominator applies to both expressions. This means that by studying only the numerators, we find out that the expected score for player A is QA / QB times greater than the expected score for player B. It then follows that for each 400 rating points of advantage over the opponent, the chance of winning is magnified ten times in comparison to the opponent’s chance of winning.
Also note that EA + EB = 1. In practice, since the true strength of each player is unknown, the expected scores are calculated using the player’s current ratings.
When a player’s actual tournament scores exceed his expected scores, the Elo system takes this as evidence that player’s rating is too low, and needs to be adjusted upward. Similarly when a player’s actual tournament scores fall short of his expected scores, that player’s rating is adjusted downward. Elo’s original suggestion, which is still widely used, was a simple linear adjustment proportional to the amount by which a player overperformed or underperformed his expected score. The maximum possible adjustment per game (sometimes called the K-value) was set at K = 16 for masters and K = 32 for weaker players.
Supposing Player A was expected to score EA points but actually scored SA points. The formula for updating his rating is
This update can be performed after each game or each tournament, or after any suitable rating period. An example may help clarify. Suppose Player A has a rating of 1613, and plays in a five-round tournament. He loses to a player rated 1609, draws with a player rated 1477, defeats a player rated 1388, defeats a player rated 1586, and loses to a player rated 1720. His actual score is (0 + 0.5 + 1 + 1 + 0) = 2.5. His expected score, calculated according to the formula above, was (0.506 + 0.686 + 0.785 + 0.539 + 0.351) = 2.867. Therefore his new rating is (1613 + 32· (2.5 – 2.867)) = 1601, assuming that a K factor of 32 is used.
Note that while two wins, two losses, and one draw may seem like a par score, it is worse than expected for Player A because his opponents were lower rated on average. Therefore he is slightly penalized. If he had scored two wins, one loss, and two draws, for a total score of three points, that would have been slightly better than expected, and his new rating would have been (1613 + 32· (3 – 2.867)) = 1617.
This updating procedure is at the core of the ratings used by FIDE, USCF, Yahoo! Games, the ICC, and FICS. However, each organization has taken a different route to deal with the uncertainty inherent in the ratings, particularly the ratings of newcomers, and to deal with the problem of ratings inflation/deflation. New players are assigned provisional ratings, which are adjusted more drastically than established ratings.
The principles used in these rating systems can be used for rating other competitions—for instance, international football matches.
Elo ratings have also been applied to games without the possibility of draws, and to games in which the result can also have a quantity (small/big margin) in addition to the quality (win/loss). See go rating with Elo for more.
Mathematical issues
There are three main mathematical concerns relating to the original work of Professor Elo, namely the correct curve, the correct K-factor, and the provisional period crude calculations.
Most accurate distribution model
The first mathematical concern addressed by the USCF was the use of the normal distribution. They found that this did not accurately represent the actual results achieved by particularly the lower rated players. Instead they switched to a logistical distribution model, which the USCF found provided a better fit for the actual results achieved. FIDE still uses the normal distribution as the basis for rating calculations as suggested by Elo himself. [11]
Most accurate K-factor
The second major concern is the correct « K-factor » used. The chess statistician Jeff Sonas reckons that the original K=10 value (for players rated above 2400) is inaccurate in Elo’s work. If the K-factor coefficient is set too large, there will be too much sensitivity to just a few, recent events, in terms of a large number of points exchanged in each game. Too low a K-value, and the sensitivity will be minimal, and the system will not respond quickly enough to changes in a player’s actual level of performance.
Elo’s original K-factor estimation was made without the benefit of huge databases and statistical evidence. Sonas indicates that a K-factor of 24 (for players rated above 2400) may be more accurate both as a predictive tool of future performance, and also more sensitive to performance.
Certain Internet chess sites seem to avoid a three-level K-factor staggering based on rating range. For example the ICC seems to adopt a global K=32 except when playing against provisionally rated players. The USCF (which makes use of a logistic distribution as opposed to a normal distribution) has staggered the K-factor according to three main rating ranges of:
- Players below 2100 -> K factor of 32 used
- Players between 2100 and 2400 -> K factor of 24 used
- Players above 2400 -> K factor of 16 used
FIDE uses the following ranges:
- K = 25 for a player new to the rating list until he has completed events with a total of at least 30 games.
- K = 15 as long as a player’s rating remains under 2400.
- K = 10 once a player’s published rating has reached 2400, and he has also completed events with a total of at least 30 games. Thereafter it remains permanently at 10.
In over-the-board chess, the staggering of the K-factor is important to ensure minimal inflation at the top end of the rating spectrum. This assumption might in theory apply equally to an online chess server, as well as a standard over-the-board chess organisation such as FIDE or USCF. In theory, it would make it harder for players to get much higher ratings if their K-factor was reduced when they got over 2400 rating. However, the ICC’s help on K-factors indicates [14] that it may simply be the choosing of opponents that enables 2800+ players to further increase their rating quite easily. This would seem to hold true, for example, if one analysed the games of a grandmaster on the ICC: one can find a string of games of opponents who are all over 3100. In over-the-board chess, it would only be in very high level all-play-all events that this player would be able to find a steady stream of 2700+ opponents – in at least a category 15+ FIDE event. A category 10 FIDE event would mean players are restricted in rating between 2476 to 2500. However, if the player entered normal Swiss-paired open over-the-board chess tournaments, he would likely meet many opponents less than 2500 FIDE on a regular basis. A single loss or draw against a player rated less than 2500 would knock the GM’s FIDE rating down significantly.
Even if the K-factor was 16, and the player defeated a 3100+ player several games in a row, his rating would still rise quite significantly in a short period of time, due to the speed of blitz games, and hence the ability to play many games within a few days. The K-factor would arguably only slow down the increases that the player achieves after each win. The evidence given in the ICC K-factor article relates to the auto-pairing system, where the maximum ratings achieved are seen to be only about 2500. So it seems that random-pairing as opposed to selective pairing is the key for combatting rating inflation at the top end of the rating spectrum, and possibly only to a much lesser extent, a slightly lower K-factor for a player >2400 rating.
Practical issues
Game activity versus protecting one’s rating
In general the Elo system has increased the competitive climate for chess and inspired players for further study and improvement of their game. However, in some cases ratings can discourage game activity for players who wish to « protect their rating ».Examples:
- They may choose their events or opponents more carefully where possible.
- If a player is in a Swiss tournament, and loses a couple of games in a row, they may feel the need to abandon the tournament in order to avoid any further rating « damage ».
- Junior players, who may have high provisional ratings, might play less than they would, because of rating concerns.
In these examples, the rating « agenda » can sometimes conflict with the agenda of promoting chess activity and rated games.
Interesting from the perspective of preserving high Elo ratings versus promoting rated game activity is a recent proposal by British Grandmaster John Nunn regarding qualifiers based on Elo rating for a World championship model.> Nunn highlights in the section on « Selection of players », that players not only be selected by high Elo ratings, but also their rated game activity. Nunn clearly separates the « activity bonus » from the Elo rating, and only implies using it as a tie-breaking mechanism.
Selective pairing
A more subtle issue is related to pairing. When players can choose their own opponents, they can choose opponents with minimal risk of losing, and maximum reward for winning. Such a luxury of being able to hand-pick your opponents is not present in Over-the-Board Elo type calculations, and therefore this may account strongly for the ratings on the ICC using Elo which are well over 2800.
Particular examples of 2800+ rated players choosing opponents with minimal risk and maximum possibility of rating gain include: choosing computers that they know they can beat with a certain strategy; choosing opponents that they think are over-rated; or avoiding playing strong players who are rated several hundred points below them, but may hold chess titles such as IM or GM. In the category of choosing over-rated opponents, new-entrants to the rating system who have played less than 50 games are in theory a convenient target as they may be overrated in their provisional rating. The ICC compensates for this issue by assigning a lower K-factor to the established player if they do win against a new rating entrant. The K-factor is actually a function of the number of rated games played by the new entrant.
Therefore, Elo ratings online still provide a useful mechanism for providing a rating based on the opponent’s rating. Its overall credibility, however, needs to be seen in the context of at least the above two major issues described — engine abuse, and selective pairing of opponents.
The ICC has also recently introduced « auto-pairing » ratings which are based on random pairings, but with each win in a row ensuring a statistically much harder opponent who has also won x games in a row. With potentially hundreds of players involved, this creates some of the challenges of a major large Swiss event which is being fiercely contested, with round winners meeting round winners. This approach to pairing certainly maximizes the rating risk of the higher-rated participants, who may face very stiff opposition from players below 3000 for example. This is a separate rating in itself, and is under « 1-minute » and « 5-minute » rating categories. Maximum ratings achieved over 2500 are exceptionally rare.
Ratings inflation and deflation
An increase or decrease in the average rating over all players in the rating system is often referred to as rating inflation or rating deflation respectively. For example, if there is inflation, a modern rating of 2500 means less than a historical rating of 2500, while the reverse is true if there is deflation. Using ratings to compare players between different eras is made more difficult when inflation and deflation is present. (See also Greatest chess player of all time.)
It is commonly believed that, at least at the top level, modern ratings are inflated. For instance Nigel Short said in September 2009, « The recent ChessBase article on rating inflation by Jeff Sonas would suggest that my rating in the late 1980s would be approximately equivalent to 2750 in today’s much debauched currency« . (Short’s highest rating in the 1980s was 2665 in July 1988, which was equal third in the world. When he made this comment, 2665 would have ranked him 65th, while 2750 would have ranked him equal 10th).
It has been suggested that an overall increase in ratings reflects greater skill. The advent of strong chess computers allows a somewhat objective evaluation of the absolute playing skill of past chess masters, based on their recorded games, but this is also a measure of how computerlike the players’ moves are, not merely a measure of how strongly they have played.
The number of people with ratings over 2700 has increased. Around 1979 there was only one active player ( Anatoly Karpov) with a rating this high. This increased to 15 players in 1994, while 33 players have this rating in 2009, which has made this top echelon of chess mastery less exclusive. One possible cause for this inflation was the rating floor, which for a long time was at 2200, and if a player dropped below this they were stricken from the rating list. As a consequence, players at a skill level just below the floor would only be on the rating list if they were overrated, and this would cause them to feed points into the rating pool.
In 1995, the USCF experienced that several young scholastic players were improving faster than what the rating system was able to track. As a result, established players with stable ratings started to lose rating points to the young and underrated players. Several of the older established players were frustrated over what they considered an unfair rating decline, and some even quit chess over it.
Combating deflation
Because of the significant difference in timing of when inflation and deflation occur, and in order to combat deflation, most implementations of Elo ratings have a mechanism for injecting points into the system in order to maintain relative ratings over time. FIDE has two inflationary mechanisms. First, performances below a « ratings floor » are not tracked, so a player with true skill below the floor can only be unrated or overrated, never correctly rated. Second, established and higher-rated players have a lower K-factor. New players have a K=25, which drops to K=15 after 30 played games, and to K=10 when the player reaches 2400.
The current system in the United States includes a bonus point scheme which feeds rating points into the system in order to track improving players, and different K-values for different players. Some methods, used in Norway for example, differentiate between juniors and seniors, and use a larger K factor for the young players, even boosting the rating progress by 100% for when they score well above their predicted performance.
Rating floors in the USA work by guaranteeing that a player will never drop below a certain limit. This also combats deflation, but the chairman of the USCF Ratings Committee has been critical of this method because it does not feed the extra points to the improving players. (A possible motive for these rating floors is to combat sandbagging, i.e. deliberate lowering of ratings to be eligible for lower rating class sections and prizes.)
Other chess rating systems
- Ingo system, designed by Anton Hoesslinger, used in Germany 1948-1992 ( Harkness 1967:205–6).
- Harkness System, invented by Kenneth Harkness, who published it in 1956 ( Harkness 1967:185–88).
- British Chess Federation Rating System, published in 1958, now termed the ECF grading system.
- Correspondence Chess League of America Rating System (now uses Elo).
- Glicko rating system
- Chessmetrics
- In November 2005, the Xbox Live online gaming service proposed the TrueSkill ranking system that is an extension of Glickman’s system to multi-player and multi-team games.
Elo ratings in other games
American Collegiate Football uses the Elo method as a portion of its Bowl Championship Series rating systems. Jeff Sagarin of USA Today publishes team rankings for most American sports, including Elo system ratings for College Football. The NCAA uses his Elo ratings as part of a formula to determine the annual participants in the College Football National Championship Game.
National Scrabble organizations compute normally-distributed Elo ratings except in the United Kingdom, where a different system is used. The North American National Scrabble Association has the largest rated population, numbering over 11,000 as of early 2006. Lexulous also uses the Elo system.
The popular First Internet Backgammon Server calculates ratings based on a modified Elo system. New players are assigned a rating of 1500, with the best humans and bots rating over 2000. The same formula has been adopted by several other backgammon sites, such as Play65, DailyGammon, GoldToken and VogClub. VogClub sets a new player’s rating at 1600.
The European Go Federation adopted an Elo based rating system initially pioneered by the Czech Go Federation.
In other sports, individuals maintain rankings based on the Elo algorithm. These are usually unofficial, not endorsed by the sport’s governing body. The World Football Elo Ratings rank national teams in men’s football. In 2006, Elo ratings were adapted for Major League Baseball teams by Nate Silver of Baseball Prospectus. Based on this adaptation, Baseball Prospectus also makes Elo-based Monte Carlo simulations of the odds of whether teams will make the playoffs. One of the few Elo-based rankings endorsed by a sport’s governing body is the FIFA Women’s World Rankings, based on a simplified version of the Elo algorithm, which FIFA uses as its official ranking system for national teams in women’s football.
Various online role-playing games use Elo ratings for player-versus-player rankings. In Guild Wars, Elo ratings are used to record guild rating gained and lost through Guild versus Guild battles, which are two-team fights. The initial K-value was 30, but was changed to 5 in January 2007, then changed to 15 in July 2009. Vendetta Online uses Elo ratings to rank the flight combat skill of players when they have agreed to a one-on-one duel. World of Warcraft formerly used the Elo Rating system when teaming up and comparing Arena players, but now uses a system similar to Microsoft’s TrueSkill. Starcraft 2 also uses a modified Elo rating system, having added a hidden rating mechanic. The game Puzzle Pirates uses the Elo rating system as well to determine the standings in the various puzzles. Also Roblox introduced the Elo rating in 2010. League of Legends, Heroes of Newerth and Bloodline Champions use modified Elo rating systems to rank individuals in a team-based environment. UniWar also uses the Elo system to give players scores based on their competitive results. For the third expansion Retribution of Dawn of War 2 THQ switched from Microsofts TrueSkill to the ELO-System.
Despite questions of the appropriateness of using the Elo system to rate games in which luck is a factor, trading-card game manufacturers often use Elo ratings for their organized play efforts. The DCI (formerly Duelists’ Convocation International) uses Elo ratings for tournaments of Magic: The Gathering and other games of Wizards of the Coast. Pokémon USA uses the Elo system to rank its TCG organized play competitors. Prizes for the top players in various regions include holidays and world championships invites. Similarly, Decipher, Inc. used the Elo system for its ranked games such as Star Trek Customizable Card Game and Star Wars Customizable Card Game.
[/lang_en]